Um dos motivos para introduzir a decomposição LU é que ela fornece uma maneira eficiente de calcular a matriz inversa, a qual tem muitas aplicações na engenharia; ela também fornece um meio de avaliar o condicionamento do sistema.

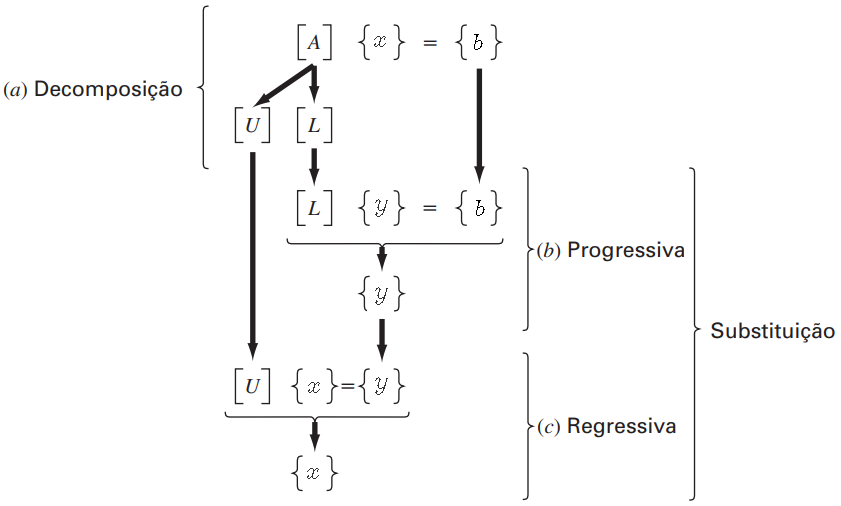
A decomposição pode ser dividida em dois passos:

$1$ – Passo de decomposição: a matriz $A$ é fatorada em duas matrizes triangulares, uma inferior $L$ com elementos da diagonal principal iguais a $1$, e uma superior $U,$ onde, realizando a multiplicação $L\times U$, obtemos a matriz $A$.

$2$ – Resolução do sistema: $L$ e $U$ são usadas para determinar a solução do sistema, $x$, através do processo: $$ Ax = b. $$ Se $A = LU$, então $LUx = y$. Defina um vetor de incógnitas auxiliar, $y$: $$L\underset{y}{\underbrace{Ux}} = b,$$ ou seja, $$ Ux = y. $$ Logo, $$ Ly = b. $$ Observe que no sistema acima, $L$ é uma matriz triangular inferior, $b$ é a matriz de termos independentes do sistema original e $y$ é o vetor de incognitas auxiliar. Resolvendo $Ly=b$ usando substituição progressiva, podemos usar a relação $Ux=y$ para encontrar $x$ por substituição regressiva, já que $U$ é triangular superior.

A ilustração a seguir nos dá uma boa representação:

Veremos a seguir, como podemos obter as matrizes Lower e Upper a partir do Método da Eliminação de Gauss. Para isso, vamos usar a mesma matriz que vimos no Método de Eliminação de Gauss.

Seja um sistema linear:

Podemos escrevê-lo na forma matricial do tipo $Ax$ = $b$, onde: Após isso, iremos decompor a matriz de coeficientes $A$ em duas matrizes, uma triangular inferior e outra triangular superior $L$ e $U$, respectivamente.

Para que uma matriz tenha decomposição LU, o determinante de todos os seus menores principais devem ser diferentes de zero. Vamos checar essa condição para nossa matriz A:

Primeiro menor principal: $$\det \left([3]\right) = 3 \neq 0$$ Segundo menor principal: Agora que sabemos que a matriz de coeficientes pode ser decomposta, vamos começar fazendo a Eliminação de Gauss. Porém, dessa vez, iremos guardar os fatores $f_{ij}$ usados para zerar os elementos que ficam abaixo do pivô.

Primeiramente vamos supor uma matriz $L$ de dimensão $3 \times 3$ triangular inferior do tipo: $$ L =\begin{bmatrix}1 & 0 & 0 \\ f{21} & 1 & 0 \\ f{31} & f{32} & 1 \end{bmatrix}. $$ Obteremos o valor desses fatores durante a Eliminação de Gauss.

O fator $f_{21}$ é o fator utilizado na Eliminação de Gauss para zerar o elemento da segunda linha que está abaixo do primeiro pivô. Para a matriz $A$, obtemos da seguinte maneira: $$f_{21} = \frac{A(2,1)}{A(1,1)}= \frac{1}{3}$$ Para zerar o elemento abaixo do pivô fazemos: $$L_2 = L_2 – f_{21}L1.$$ Logo, $$ A = \begin{bmatrix} 3 & 2 & 4 & \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 4 & 3 & -2 \end{bmatrix}. $$ De maneira similar obtemos o fator $f_{31}$, que será o fator utilizado para zerar o elemento da terceira linha que está abaixo do primeiro pivô. $$f_{31} = \frac{A(3,1)}{A(1,1)} = \frac{4}{3}.$$ Para zerar o elemento fazemos: $$L_3 = L_3 – f_{31}L_1.$$ Logo, $$ A =\begin{bmatrix}3 & 2 & 4 \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & \frac{1}{3} & -\frac{22}{3} \end{bmatrix}. $$ Por fim, como todos os elementos abaixo do primeiro pivô $A_{11}$ estão zerados, temos agora como pivô o elemento $A_{22}$ e precisamos zerar o que está abaixo dele: $$f_{32} = \frac{A_{32}}{A_{22}} = \frac{\frac{1}{3}}{\frac{1}{3}} = 1$$ Para zerar o elemento: $$L_3 = L_3 – f_{32}L_2.$$ Assim, $$ A =\begin{bmatrix}3 & 2 & 4 \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & -8 \end{bmatrix}. $$ A matriz triangular superior obtida no final da Eliminação de Gauss é chamada de matriz $U$. Já a matriz $L$ será a matriz triangular inferior que contém os elementos da diagonal principal iguais a $1$, além dos fatores que utilizamos para zerar os elementos, como vimos acima. Por fim, podemos verificar que, de fato, $LU = A$: Agora que decompomos a nossa matriz $A$ nas matrizes $L$ e $U$, podemos usá-las para obter a solução do sistema linear do exemplo. Temos que:
$$ Ax = b $$ Substituindo a matriz $A$ pelas matrizes $LU$ obtidas: O que temos acima é $LUx = b$. Agora usaremos o vetor de incógnitas auxiliar, $y$. Definindo $Ux=y$, temos que $Ly = b$, ou seja, O sistema acima é do tipo triangular inferior, cuja forma de resolver já estudamos anteriormente: $$ y_{1} = 1 $$ $$ y_{2} = 2 - \frac{1}{3} * y_{1} = \frac{5}{3} $$ $$ y_{3} = 3 - \frac{4}{3}y_{1} - y_{2} = 0 . $$ Agora retornamos a nossa relação $Ux = y$: $$ \begin{bmatrix}3 & 2 & 4 \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & -8 \end{bmatrix} \begin{bmatrix}x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \space \begin{bmatrix}1 \\ \frac{5}{3} \\ 0 \end{bmatrix}. $$ Para encontrar finalmente o valor de $x$, precisamos resolvar o sistema triangular superior acima. Logo: $$ x_{3} = 0, $$ $$ x_{2} = \frac{\frac{5}{3} - \frac{2}{3}*0}{\frac{1}{3}} = 5, $$ que é a solução do sistema.

Suponha que queremos determinar a inversa da matriz $A$ do exemplo acima. Como já calculamos a decomposição $LU$ dessa matriz, o processo de determinação da inversa se torna direto.

Vamos calcular cada coluna da inversa individualmente. A primeira coluna da matriz inversa vai ser dada pela solução do sistema: $$Ad_1 = I_1$$ Onde $d_1$ é a primeira coluna da inversa de $A$ e $I_1$ a primeira coluna da matriz identidade de dimensões iguais as de $A$. Temos que: $$ \begin{bmatrix}3 & 2 & 4 \\ 1 & 1 & 2 \\ 4 & 3 & -2 \end{bmatrix} \space \begin{bmatrix} d_{11} \\ d_{12}\\ d_{13} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} $$ Como temos a decomposição da $LU$ da matriz $A$, podemos resolver o sistema em duas partes como vimos no exemplo acima; fazemos a substituição $Ud_1 = y$ e calculamos primeiramente $Ly_1 = I_1$: $$ \begin{bmatrix}1 & 0 & 0 \\ \frac{1}{3} & 1 & 0 \\ \frac{4}{3} & 1 & 1 \end{bmatrix}\space \begin{bmatrix} y_{11} \\ y_{12} \\ y_{13} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} $$ Podemos resolver diretamente: $$y_{11} = 1 \\ y_{12} = -\frac{1}{3}y_{11} = -\frac{1}{3} \\ y_{13} = -\frac{4}{3}y_{11} - y_{12} = -1 $$ Agora, resolvemos o sistema $Ud_1 = y_1$: $$\begin{bmatrix}3 & 2 & 4 \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & -8 \end{bmatrix} \space \begin{bmatrix} d_{11} \\ d_{12} \\ d_{13} \end{bmatrix} = \begin{bmatrix} 1 \\ -\frac{1}{3}\\ -1\end{bmatrix}$$ $$ d_{13} = \frac{-1}{-8} = 0.125\\ d_{12} = \frac{-\frac{1}{3} - \frac{2}{3}d_{13}}{\frac{1}{3}} = -1.25 \\ d_{11} = \frac{1-2d_{12} - 4d_{13}}{3} = 1 $$ Ou seja, a primeira coluna da inversa de $A$ é dada por: $$d_1 = \begin{bmatrix} 1\\ -1.25 \\ 0.125 \end{bmatrix} $$ Obtemos a segunda coluna de maneira similar: $$ \begin{bmatrix}3 & 2 & 4 \\ 1 & 1 & 2 \\ 4 & 3 & -2 \end{bmatrix} \space \begin{bmatrix} d_{21} \\ d_{22}\\ d_{23} \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} $$ $$ \begin{bmatrix}1 & 0 & 0 \\ \frac{1}{3} & 1 & 0 \\ \frac{4}{3} & 1 & 1 \end{bmatrix} \space \begin{bmatrix} y_{21} \\ y_{22} \\ y_{23} \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} $$ $$ y_{21} = 0 \\ y_{22} = 1 \\ y_{23} = -1y_{22} = -1 $$ $$ \begin{bmatrix}3 & 2 & 4 \\ 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & -8 \end{bmatrix} \space \begin{bmatrix} d_{21} \\ d_{22} \\ d_{23} \end{bmatrix} = \begin{bmatrix} 0 \\ 1\\ -1\end{bmatrix} $$ $$ d_{23} = \frac{-1}{-8} = 0.125 \\ d_{22} = \frac{1 - \frac{2}{3}d_{23}}{\frac{1}{3}} = 2.75 \\ d_{21} = \frac{-2d_{22} - 4d_{23}}{3} = -2 $$ $$ d_2 = \begin{bmatrix} -2 \\ 2.75\\ 0.125 \end{bmatrix} $$ Repetindo os passos acima, obtemos que $$d_3 = \begin{bmatrix} 0 \\ 0.25 \\ -0.125 \end{bmatrix} $$

Para verificar o resultado, é só verificar que $AA^{-1}=A^{-1}A$, que é igual a matriz identidade $I$.