Bem vindo(a),
Visitante
Tamanho atual da fonte:
Vídeoaula
Secante - Introdução
No método de Newton precisamos calcular a derivada da função, o que pode
ser inconveniente. O método da Secante é uma alternativa ao método de Newton, onde se faz
uso de uma reta secante como uma aproximação da reta tangente em um determinado ponto.
Método da Secante
Deseja-se encontrar um valor específico de $x$ que satisfaz a equação
$$
f(x) = 0.
$$
No método da secante são necessários dois chutes iniciais para que uma nova estimativa da raiz
seja determinada. Através de uma análise (ex. gráfica), encontramos dois valores,
$x_0$ e $x_1$, que sejam próximos o suficiente da raiz procurada. A próxima estimativa da raiz,
$x_2$, é a abscissa do ponto de intersecção entre o eixo $X$ e a reta que passa pelos pontos
$(x_0,f(x_0))$ e $(x_1,f(x_1))$, conforme ilustração abaixo.
O valor de $x_2$ é obtido por análise trigonométrica:
O procedimento é repetido até que o critério de parada seja satisfeito, ou seja, até que: $$ E_r = \left|\frac{x_{n+1}-x_n}{x_{n+1}}\right| < \epsilon. $$
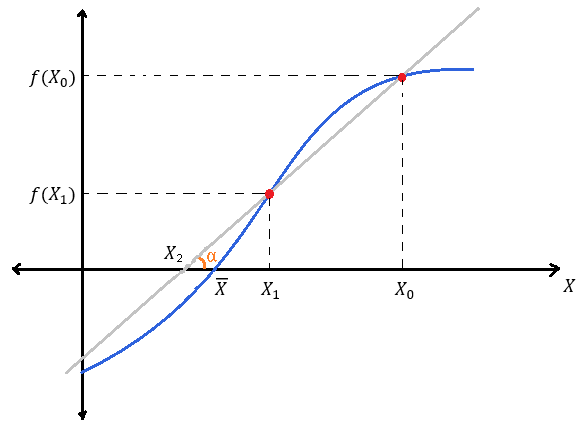
O valor de $x_2$ é obtido por análise trigonométrica:
$$\tan(\alpha) = \frac{f(x_{1})}{x_{1}\,- \; x_{2}}. $$
Isolando $x_2$:
$$x_{2} = x_{1} - \frac{f(x_{1})}{\tan(\alpha) }.$$
O valor de $\tan (\alpha)$ pode ser escrito como:
$$\; \tan (\alpha)= \frac{f(x_{0})\;-\;f(x_{1})}{x_{0}\, -\;x_{1} }.$$
Então, para cada iteração do método, encontra-se a próxima aproximação da raiz da seguinte forma:
$$x_{n+1} = x_{n}- \frac{f(x_{n}) \cdot (x_{n-1} -x_{n})}{f(x_{n-1})-f(x_{n})}.$$
O procedimento é repetido até que o critério de parada seja satisfeito, ou seja, até que: $$ E_r = \left|\frac{x_{n+1}-x_n}{x_{n+1}}\right| < \epsilon. $$
Exemplo
Utilizar método de Newton para encontrar aproximação da raiz para a função $x^{2} +x -5$ com critério de parada $E_{r} < 0.03$.
Estimativa inicial
Primeiramente, fazemos uma análise gráfica para encontrar dois pontos iniciais relativamente próximos da raiz.
Escolhemos $x_{0}=3.01$ e $x_{1}=3$.
Iteração $1$
Encontrar o valor aproximado de $\overline x$:
Calculando o erro relativo para verificar o critério de parada:
Como o critério não foi satisfeito, o método continua.
Iteração $2$
Encontrar $\;x_{3}$:
Calculando o erro:
Logo o método continua.
Iteração $3$
Encontrar $\;x_{4}$:
Calculando o erro:
Chegando na precisão desejada.
A raiz aproximada então é $\;x\;= 1.79313$.
Estimativa inicial
Primeiramente, fazemos uma análise gráfica para encontrar dois pontos iniciais relativamente próximos da raiz.
Escolhemos $x_{0}=3.01$ e $x_{1}=3$.
Iteração $1$
Encontrar o valor aproximado de $\overline x$:
$$
\begin{aligned}
x_{2} &= x_{1}- \frac{f(x_{1}) (x_{0} -x_{1})}{f(x_{0})-f(x_{1})} \\
&=3- \frac{7\cdot 0.01}{7,0701-7} \\
&= 3 - 0,99857 = 2,00143
\end{aligned}
$$
Calculando o erro relativo para verificar o critério de parada:
$$
\begin{aligned}
E_{r} &= \left| \frac{x_2 -x_1}{x_2}\right| \\
&= \left|\frac{2,00143-3}{2,00143}\right| > 0.03 \\
\end{aligned}
$$
Como o critério não foi satisfeito, o método continua.
Iteração $2$
Encontrar $\;x_{3}$:
$$
\begin{aligned}
x_{3} &= x_{2}- \frac{f(x_{2}) (x_{1} -x_{2})}{f(x_{1 })-f(x_{2})}\\
&= 2,00143 - \frac{1,00714 \cdot 0,99857}{7 -1,00714} \\
&= 1,83361 \\
\end{aligned}
$$
Calculando o erro:
$$
\begin{aligned}
E_{r} &= \left| \frac{x_3 -x_2}{x_3}\right| \\
&= \left|\frac{1,83361-2,00143}{1,83361}\right| > 0.03 \\
\end{aligned}
$$
Logo o método continua.
Iteração $3$
Encontrar $\;x_{4}$:
$$
\begin{aligned}
x_{4} &= x_{3}- \frac{f(x_{3}) (x_{2}-x_{3})}{f(x_{2})-f(x_{3})}\\
&= 1,83361- \frac{0,19574 \cdot 0,16782}{1,00713-0,19574} \\
&= 1,79313 \\
\end{aligned}
$$
Calculando o erro:
$$
\begin{aligned}
E_{r} &= \left| \frac{x_4 -x_3}{x_4}\right| \\
&= \left|\frac{1,79313-1,83361}{1,79313}\right| < 0.03 \\
\end{aligned}
$$
Chegando na precisão desejada.
A raiz aproximada então é $\;x\;= 1.79313$.
Exemplo com Geogebra
Use o método da secante para encontrar a raiz positiva da equação abaixo com $E_r < 0.01$.
$$ \frac{x^2}{5} - 2x = 3.$$
Solução:
- Fazendo-se uma análise gráfica, podemos usar $x_0 = 11.9$ e $x_1 = 11.7$ como chutes iniciais.
Algoritmo para implementação computacional